
Actual Windows Guard v1.5 serial key or number

Actual Windows Guard v1.5 serial key or number
Windows key


The Windows logo key (also known as Windows-, win-,start-, logo-, flag-, or super- key[1]) is a keyboard key which was originally introduced on the Microsoft Natural keyboard in 1994.[2] This key became a standard key on PC keyboards. In Windows tapping the key brings up the start menu. + performs the same function, in case the keyboard lacks this key.
History and usage[edit]
Historically, the addition of two Windows keys and a menu key marked the change from the 101/102-key to 104/105-key layout for PC keyboards.[3] Compared to the former layout, a Windows key was placed between the left and the left and another Windows key and the menu key were placed between the right (or ) and the right key.
The key is predated by the key on Apple computers in 1980 and the key in LISP/UNIX computers in 1970.
In laptop and other compact keyboards it is common to have just one Windows key (usually on the left). On Microsoft's Entertainment Desktop sets (designed for Windows Vista), the Windows key is in the middle of the keyboard, below all other keys (where the user's thumbs rest).
On Windows 8 tablet computers, hardware certification requirements initially mandated that the Windows key be centered on the bezel below the screen, except on a convertible laptop, where the button is allowed to be off-center in a tablet configuration. This requirement was relaxed in Windows 8.1, allowing the Windows key to be placed on any bezel or edge of the unit, though a centered location along the bottom bezel is still preferred.[4]
Licensing[edit]
Microsoft regulates the appearance of the Windows key logo picture with a specially crafted license for keyboard manufacturers ("Microsoft Windows Logo Key Logo License Agreement for Keyboard Manufacturers"). With the introduction of a new Microsoft Windows logo, first used with Windows XP, the agreement was updated to require that the new design be adopted for all keyboards manufactured after 1 September 2003.[5] However, with the release of Windows Vista, Microsoft published guidelines for a new Windows Logo key that incorporates the Windows logo recessed in a chamfered lowered circle with a contrast ratio of at least 3:1 with respect to background that the key is applied to.[6]
In Common Building Block Keyboard Specification, all CBB compliant keyboards were to comply with the Windows Vista Hardware Start Button specification beginning in 1 June 2007.[citation needed]
Wikipedia uses the Unicode character U+229E ⊞SQUARED PLUS as a simulation of the logo.
Use with Microsoft Windows[edit]
On Windows 9x and Windows NT families of Windows operating system, tapping the Windows key by itself traditionally revealed Windows Taskbar (if not visible) and opened the Start menu. In Windows Server 2012 and Windows 8, this key launches the Start screen but doesn't show the taskbar. However, this feature was added back into Windows 10.
Pressing the key in combination with other keys allows invoking many common functions through the keyboard. Holding down + will not substitute for the Windows key in these combinations. Which Windows key combinations ("shortcuts") are available and active in a given Windows session depends on many factors, such as accessibility options, the type of the session (regular or Terminal Services), the Windows version, the presence of specific software such as IntelliType and Group Policy if applicable.
Below is a list of notable shortcuts. Unless otherwise noted, they are valid in the next version of Windows.
Windows 95 and Windows NT 4.0[edit]
The following shortcuts are valid in Windows 95 and Windows NT 4.0.[7][8]
- opens the Start Menu
- + shows the desktop (hiding even non-minimizable windows), or restores hidden windows when pressed a second time.
- + opens Windows Explorer with folder pane on left side of window.
- + opens Find files and folders.
- + minimizes all windows.
- ++ restores windows that were minimized with +.
- + opens the "Run Program Or File" Window.
- + runs Utility Manager.
- + or + opens properties of My Computer.
- + opens Windows Help.
- ++ opens Find computers.
- + cycles through taskbar buttons. This key combination is reassigned in Windows Vista.
Windows 2000[edit]
Windows 2000 adds the following:
Windows XP[edit]
Windows XP adds the following:
Windows XP Media Center Edition[edit]
Windows XP Media Center Edition adds the following:
Windows Vista[edit]
Windows Vista adds the following shortcuts:
- + brings the Windows Sidebar to the front.
- + selects next Windows Sidebar gadget item, bringing all gadgets to the foreground in process. Gadgets were discontinued in Windows 8.
- + invokes Windows Mobility Center. Works only if portable computer features are installed. This key combination is reassigned in Windows 8.
- + switches active app using Aero Flip 3D. Requires desktop composition, a feature of Windows Aero. Aero Flip 3D is discontinued in Windows 8 and this key is reassigned.
- ++ is same as above, but Aero Flip 3D remains even when this key combination is released. Arrow keys or mouse may be used to navigate between windows.
- + through +, + starts the corresponding Quick Launch Bar program. + runs the tenth item. Quick Launch is discontinued in Windows 7, but later continued from Windows 8 onward.
Windows 7[edit]
Windows 7 used the following shortcuts:
- + activates Aero Peek. Reassigned in Windows 8.
- + toggles between the devices that receive video card's output. The default is computer monitor only. Other options are video projector only, both showing the same image and both showing a portion of a larger desktop.
- + maximizes the active window.
- + restores the default window size and state of the active window, if maximized. Otherwise, minimizes the active window.
- + or to align the window to the corresponding side of the screen, tiled vertically.
- ++ or to move the window to the next or previous monitor, if multiple monitors are used.
- + to iterate through items on the taskbar from left to right.
- ++ to iterate through items on the taskbar from right to left.
- + to zoom into the screen at the mouse cursor position using the Magnifier Utility.
- + to zoom out if the Magnifier Utility is running.
- + to exit zoom.
- + through +, + to either start or switch to the corresponding program pinned to taskbar. + runs the tenth item. Press multiple times to cycle through the application's open windows. Press and release quickly to keep the taskbar's preview open (which allows you to cycle using arrow keys).
- + minimizes all windows other than the active window. Pressing this combination a second time restores them.
- + minimizes all windows. Pressing the combination a second time restores them.
- + locks the computer screen.
Windows 8[edit]
Windows 8 introduces the following:
- Opens the Start Screen (Windows 8 and 8.1 only)
- + opens the charms.
- + opens Search charm in file mode to search for computer files. If the Search charm is already open, switches to file search mode.
- + opens Search charm in settings mode to search for Control Panel
Manage Windows Defender Credential Guard
Applies to
- Windows 10 <=1903 Enterprise and Education SKUs
- Windows 10 >=1909
- Windows Server 2016
- Windows Server 2019
Enable Windows Defender Credential Guard
Windows Defender Credential Guard can be enabled either by using Group Policy, the registry, or the Hypervisor-Protected Code Integrity (HVCI) and Windows Defender Credential Guard hardware readiness tool. Windows Defender Credential Guard can also protect secrets in a Hyper-V virtual machine, just as it would on a physical machine. The same set of procedures used to enable Windows Defender Credential Guard on physical machines applies also to virtual machines.
Enable Windows Defender Credential Guard by using Group Policy
You can use Group Policy to enable Windows Defender Credential Guard. This will add and enable the virtualization-based security features for you if needed.
From the Group Policy Management Console, go to Computer Configuration -> Administrative Templates -> System -> Device Guard.
Double-click Turn On Virtualization Based Security, and then click the Enabled option.
In the Select Platform Security Level box, choose Secure Boot or Secure Boot and DMA Protection.
In the Credential Guard Configuration box, click Enabled with UEFI lock, and then click OK. If you want to be able to turn off Windows Defender Credential Guard remotely, choose Enabled without lock.
In the Secure Launch Configuration box, choose Not Configured, Enabled or Disabled. Check this article for more details.
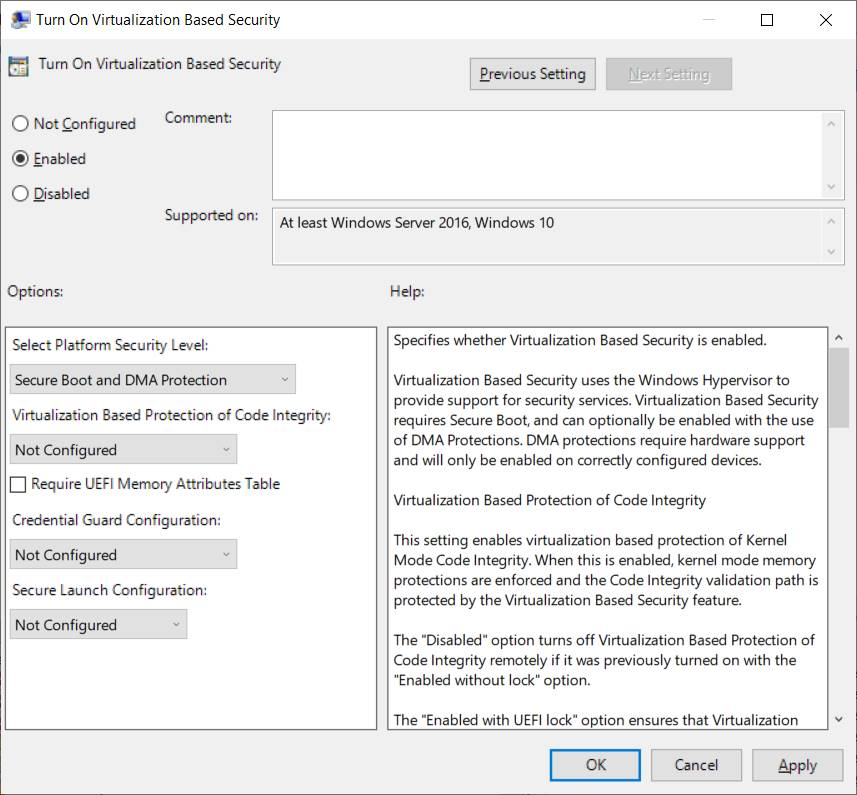
Close the Group Policy Management Console.
To enforce processing of the group policy, you can run .
Enable Windows Defender Credential Guard by using Intune
From Home, click Microsoft Intune.
Click Device configuration.
Click Profiles > Create Profile > Endpoint protection > Windows Defender Credential Guard.
Note
It will enable VBS and Secure Boot and you can do it with or without UEFI Lock. If you will need to disable Credential Guard remotely, enable it without UEFI lock.
Enable Windows Defender Credential Guard by using the registry
If you don't use Group Policy, you can enable Windows Defender Credential Guard by using the registry. Windows Defender Credential Guard uses virtualization-based security features which have to be enabled first on some operating systems.
Add the virtualization-based security features
Starting with Windows 10, version 1607 and Windows Server 2016, enabling Windows features to use virtualization-based security is not necessary and this step can be skipped.
If you are using Windows 10, version 1507 (RTM) or Windows 10, version 1511, Windows features have to be enabled to use virtualization-based security. You can do this by using either the Control Panel or the Deployment Image Servicing and Management tool (DISM).
Note
If you enable Windows Defender Credential Guard by using Group Policy, the steps to enable Windows features through Control Panel or DISM are not required. Group Policy will install Windows features for you.
Add the virtualization-based security features by using Programs and Features
Open the Programs and Features control panel.
Click Turn Windows feature on or off.
Go to Hyper-V -> Hyper-V Platform, and then select the Hyper-V Hypervisor check box.
Select the Isolated User Mode check box at the top level of the feature selection.
Click OK.
Add the virtualization-based security features to an offline image by using DISM
Open an elevated command prompt.
Add the Hyper-V Hypervisor by running the following command:
Add the Isolated User Mode feature by running the following command:
Note
In Windows 10, version 1607 and later, the Isolated User Mode feature has been integrated into the core operating system. Running the command in step 3 above is therefore no longer required.
Tip
You can also add these features to an online image by using either DISM or Configuration Manager.
Enable virtualization-based security and Windows Defender Credential Guard
Open Registry Editor.
Enable virtualization-based security:
- Go to HKEY_LOCAL_MACHINE\System\CurrentControlSet\Control\DeviceGuard.
- Add a new DWORD value named EnableVirtualizationBasedSecurity. Set the value of this registry setting to 1 to enable virtualization-based security and set it to 0 to disable it.
- Add a new DWORD value named RequirePlatformSecurityFeatures. Set the value of this registry setting to 1 to use Secure Boot only or set it to 3 to use Secure Boot and DMA protection.
Enable Windows Defender Credential Guard:
- Go to HKEY_LOCAL_MACHINE\System\CurrentControlSet\Control\LSA.
- Add a new DWORD value named LsaCfgFlags. Set the value of this registry setting to 1 to enable Windows Defender Credential Guard with UEFI lock, set it to 2 to enable Windows Defender Credential Guard without lock, and set it to 0 to disable it.
Close Registry Editor.
Note
You can also enable Windows Defender Credential Guard by setting the registry entries in the FirstLogonCommands unattend setting.
Enable Windows Defender Credential Guard by using the HVCI and Windows Defender Credential Guard hardware readiness tool
You can also enable Windows Defender Credential Guard by using the HVCI and Windows Defender Credential Guard hardware readiness tool.
Important
When running the HVCI and Windows Defender Credential Guard hardware readiness tool on a non-English operating system, within the script, change to be instead, in order for the tool to work. This is a known issue.
Review Windows Defender Credential Guard performance
Is Windows Defender Credential Guard running?
You can view System Information to check that Windows Defender Credential Guard is running on a PC.
Click Start, type msinfo32.exe, and then click System Information.
Click System Summary.
Confirm that Credential Guard is shown next to Virtualization-based security Services Configured.
Here's an example:

You can also check that Windows Defender Credential Guard is running by using the HVCI and Windows Defender Credential Guard hardware readiness tool.
Important
When running the HVCI and Windows Defender Credential Guard hardware readiness tool on a non-English operating system, within the script, change to be instead, in order for the tool to work. This is a known issue.
Note
For client machines that are running Windows 10 1703, LsaIso.exe is running whenever virtualization-based security is enabled for other features.
We recommend enabling Windows Defender Credential Guard before a device is joined to a domain. If Windows Defender Credential Guard is enabled after domain join, the user and device secrets may already be compromised. In other words, enabling Credential Guard will not help to secure a device or identity that has already been compromised, which is why we recommend turning on Credential Guard as early as possible.
You should perform regular reviews of the PCs that have Windows Defender Credential Guard enabled. This can be done with security audit policies or WMI queries. Here's a list of WinInit event IDs to look for:
- Event ID 13 Windows Defender Credential Guard (LsaIso.exe) was started and will protect LSA credentials.
- Event ID 14 Windows Defender Credential Guard (LsaIso.exe) configuration: [0x0 | 0x1 | 0x2], 0
- The first variable: 0x1 or 0x2 means that Windows Defender Credential Guard is configured to run. 0x0 means that it's not configured to run.
- The second variable: 0 means that it's configured to run in protect mode. 1 means that it's configured to run in test mode. This variable should always be 0.
- Event ID 15 Windows Defender Credential Guard (LsaIso.exe) is configured but the secure kernel is not running; continuing without Windows Defender Credential Guard.
- Event ID 16 Windows Defender Credential Guard (LsaIso.exe) failed to launch: [error code]
- Event ID 17 Error reading Windows Defender Credential Guard (LsaIso.exe) UEFI configuration: [error code]
You can also verify that TPM is being used for key protection by checking Event ID 51 in the Microsoft -> Windows -> Kernel-Boot event source. If you are running with a TPM, the TPM PCR mask value will be something other than 0.- Event ID 51 VSM Master Encryption Key Provisioning. Using cached copy status: 0x0. Unsealing cached copy status: 0x1. New key generation status: 0x1. Sealing status: 0x1. TPM PCR mask: 0x0.
You can use Windows PowerShell to determine whether credential guard is running on a client computer. On the computer in question, open an elevated PowerShell window and run the following command:
This command generates the following output:
- 0: Windows Defender Credential Guard is disabled (not running)
- 1: Windows Defender Credential Guard is enabled (running)
Note
Checking the task list or Task Manager to see if LSAISO.exe is running is not a recommended method for determining whether Windows Defender Credential Guard is running.
Disable Windows Defender Credential Guard
To disable Windows Defender Credential Guard, you can use the following set of procedures or the Device Guard and Credential Guard hardware readiness tool. If Credential Guard was enabled with UEFI Lock then you must use the following procedure as the settings are persisted in EFI (firmware) variables and it will require physical presence at the machine to press a function key to accept the change. If Credential Guard was enabled without UEFI Lock then you can turn it off by using Group Policy.
If you used Group Policy, disable the Group Policy setting that you used to enable Windows Defender Credential Guard (Computer Configuration -> Administrative Templates -> System -> Device Guard -> Turn on Virtualization Based Security).
Delete the following registry settings:
- HKEY_LOCAL_MACHINE\System\CurrentControlSet\Control\LSA\LsaCfgFlags
- HKEY_LOCAL_MACHINE\Software\Policies\Microsoft\Windows\DeviceGuard\LsaCfgFlags
If you also wish to disable virtualization-based security delete the following registry settings:
- HKEY_LOCAL_MACHINE\Software\Policies\Microsoft\Windows\DeviceGuard\EnableVirtualizationBasedSecurity
- HKEY_LOCAL_MACHINE\Software\Policies\Microsoft\Windows\DeviceGuard\RequirePlatformSecurityFeatures
Important
If you manually remove these registry settings, make sure to delete them all. If you don't remove them all, the device might go into BitLocker recovery.
Delete the Windows Defender Credential Guard EFI variables by using bcdedit. From an elevated command prompt, type the following commands:
Restart the PC.
Accept the prompt to disable Windows Defender Credential Guard.
Alternatively, you can disable the virtualization-based security features to turn off Windows Defender Credential Guard.
Note
The PC must have one-time access to a domain controller to decrypt content, such as files that were encrypted with EFS. If you want to turn off both Windows Defender Credential Guard and virtualization-based security, run the following bcdedit commands after turning off all virtualization-based security Group Policy and registry settings:
Note
Credential Guard and Device Guard are not currently supported when using Azure IaaS VMs. These options will be made available with future Gen 2 VMs.
For more info on virtualization-based security and HVCI, see Enable virtualization-based protection of code integrity.
Disable Windows Defender Credential Guard by using the HVCI and Windows Defender Credential Guard hardware readiness tool
You can also disable Windows Defender Credential Guard by using the HVCI and Windows Defender Credential Guard hardware readiness tool.
Important
When running the HVCI and Windows Defender Credential Guard hardware readiness tool on a non-English operating system, within the script, change to be instead, in order for the tool to work. This is a known issue.
Disable Windows Defender Credential Guard for a virtual machine
From the host, you can disable Windows Defender Credential Guard for a virtual machine:
What Every Computer Scientist Should Know About Floating-Point Arithmetic
Note – This appendix is an edited reprint of the paper What Every Computer Scientist Should Know About Floating-Point Arithmetic, by David Goldberg, published in the March, 1991 issue of Computing Surveys. Copyright 1991, Association for Computing Machinery, Inc., reprinted by permission.
Abstract
Floating-point arithmetic is considered an esoteric subject by many people. This is rather surprising because floating-point is ubiquitous in computer systems. Almost every language has a floating-point datatype; computers from PCs to supercomputers have floating-point accelerators; most compilers will be called upon to compile floating-point algorithms from time to time; and virtually every operating system must respond to floating-point exceptions such as overflow. This paper presents a tutorial on those aspects of floating-point that have a direct impact on designers of computer systems. It begins with background on floating-point representation and rounding error, continues with a discussion of the IEEE floating-point standard, and concludes with numerous examples of how computer builders can better support floating-point.
Categories and Subject Descriptors: (Primary) C.0 [Computer Systems Organization]: General -- instruction set design; D.3.4 [Programming Languages]: Processors -- compilers, optimization; G.1.0 [Numerical Analysis]: General -- computer arithmetic, error analysis, numerical algorithms (Secondary)
D.2.1 [Software Engineering]: Requirements/Specifications -- languages; D.3.4 Programming Languages]: Formal Definitions and Theory -- semantics; D.4.1 Operating Systems]: Process Management -- synchronization.
General Terms: Algorithms, Design, Languages
Additional Key Words and Phrases: Denormalized number, exception, floating-point, floating-point standard, gradual underflow, guard digit, NaN, overflow, relative error, rounding error, rounding mode, ulp, underflow.
Introduction
Builders of computer systems often need information about floating-point arithmetic. There are, however, remarkably few sources of detailed information about it. One of the few books on the subject, Floating-Point Computation by Pat Sterbenz, is long out of print. This paper is a tutorial on those aspects of floating-point arithmetic (floating-point hereafter) that have a direct connection to systems building. It consists of three loosely connected parts. The first section, Rounding Error, discusses the implications of using different rounding strategies for the basic operations of addition, subtraction, multiplication and division. It also contains background information on the two methods of measuring rounding error, ulps and . The second part discusses the IEEE floating-point standard, which is becoming rapidly accepted by commercial hardware manufacturers. Included in the IEEE standard is the rounding method for basic operations. The discussion of the standard draws on the material in the section Rounding Error. The third part discusses the connections between floating-point and the design of various aspects of computer systems. Topics include instruction set design, optimizing compilers and exception handling.
I have tried to avoid making statements about floating-point without also giving reasons why the statements are true, especially since the justifications involve nothing more complicated than elementary calculus. Those explanations that are not central to the main argument have been grouped into a section called "The Details," so that they can be skipped if desired. In particular, the proofs of many of the theorems appear in this section. The end of each proof is marked with the z symbol. When a proof is not included, the z appears immediately following the statement of the theorem.
Rounding Error
Squeezing infinitely many real numbers into a finite number of bits requires an approximate representation. Although there are infinitely many integers, in most programs the result of integer computations can be stored in 32 bits. In contrast, given any fixed number of bits, most calculations with real numbers will produce quantities that cannot be exactly represented using that many bits. Therefore the result of a floating-point calculation must often be rounded in order to fit back into its finite representation. This rounding error is the characteristic feature of floating-point computation. The section Relative Error and Ulps describes how it is measured.
Since most floating-point calculations have rounding error anyway, does it matter if the basic arithmetic operations introduce a little bit more rounding error than necessary? That question is a main theme throughout this section. The section Guard Digits discusses guard digits, a means of reducing the error when subtracting two nearby numbers. Guard digits were considered sufficiently important by IBM that in 1968 it added a guard digit to the double precision format in the System/360 architecture (single precision already had a guard digit), and retrofitted all existing machines in the field. Two examples are given to illustrate the utility of guard digits.
The IEEE standard goes further than just requiring the use of a guard digit. It gives an algorithm for addition, subtraction, multiplication, division and square root, and requires that implementations produce the same result as that algorithm. Thus, when a program is moved from one machine to another, the results of the basic operations will be the same in every bit if both machines support the IEEE standard. This greatly simplifies the porting of programs. Other uses of this precise specification are given in Exactly Rounded Operations.
Floating-point Formats
Several different representations of real numbers have been proposed, but by far the most widely used is the floating-point representation.1 Floating-point representations have a base  (which is always assumed to be even) and a precision p. If
(which is always assumed to be even) and a precision p. If  = 10 and p = 3, then the number 0.1 is represented as 1.00 × 10-1. If
= 10 and p = 3, then the number 0.1 is represented as 1.00 × 10-1. If  = 2 and p = 24, then the decimal number 0.1 cannot be represented exactly, but is approximately 1.10011001100110011001101 × 2-4.
= 2 and p = 24, then the decimal number 0.1 cannot be represented exactly, but is approximately 1.10011001100110011001101 × 2-4.
In general, a floating-point number will be represented as ±d.dd... d×  e, where d.dd... d is called the significand2 and hasp digits. More precisely ±d0 . d1 d2...dp-1×
e, where d.dd... d is called the significand2 and hasp digits. More precisely ±d0 . d1 d2...dp-1× e represents the number
e represents the number
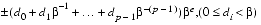 .
.The term floating-point number will be used to mean a real number that can be exactly represented in the format under discussion. Two other parameters associated with floating-point representations are the largest and smallest allowable exponents, emax and emin. Since there are  p possible significands, and emax - emin + 1 possible exponents, a floating-point number can be encoded in
p possible significands, and emax - emin + 1 possible exponents, a floating-point number can be encoded in
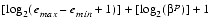
bits, where the final +1 is for the sign bit. The precise encoding is not important for now.
There are two reasons why a real number might not be exactly representable as a floating-point number. The most common situation is illustrated by the decimal number 0.1. Although it has a finite decimal representation, in binary it has an infinite repeating representation. Thus when  = 2, the number 0.1 lies strictly between two floating-point numbers and is exactly representable by neither of them. A less common situation is that a real number is out of range, that is, its absolute value is larger than
= 2, the number 0.1 lies strictly between two floating-point numbers and is exactly representable by neither of them. A less common situation is that a real number is out of range, that is, its absolute value is larger than  ×
×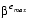 or smaller than 1.0 ×
or smaller than 1.0 ×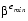 . Most of this paper discusses issues due to the first reason. However, numbers that are out of range will be discussed in the sections Infinity and Denormalized Numbers.
. Most of this paper discusses issues due to the first reason. However, numbers that are out of range will be discussed in the sections Infinity and Denormalized Numbers.
Floating-point representations are not necessarily unique. For example, both 0.01 × 101 and 1.00 × 10-1 represent 0.1. If the leading digit is nonzero (d0 0 in equation (1) above), then the representation is said to be normalized. The floating-point number 1.00 × 10-1 is normalized, while 0.01 × 101 is not. When
0 in equation (1) above), then the representation is said to be normalized. The floating-point number 1.00 × 10-1 is normalized, while 0.01 × 101 is not. When  = 2, p = 3, emin = -1 and emax = 2 there are 16 normalized floating-point numbers, as shown in FIGURE D-1. The bold hash marks correspond to numbers whose significand is 1.00. Requiring that a floating-point representation be normalized makes the representation unique. Unfortunately, this restriction makes it impossible to represent zero! A natural way to represent 0 is with 1.0 ×
= 2, p = 3, emin = -1 and emax = 2 there are 16 normalized floating-point numbers, as shown in FIGURE D-1. The bold hash marks correspond to numbers whose significand is 1.00. Requiring that a floating-point representation be normalized makes the representation unique. Unfortunately, this restriction makes it impossible to represent zero! A natural way to represent 0 is with 1.0 ×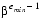 , sincethis preserves the fact that the numerical ordering of nonnegative real numbers corresponds to the lexicographic ordering of their floating-point representations.3 When the exponent is stored in a k bit field, that means that only 2k - 1 values are available for use as exponents, since one must be reserved to represent 0.
, sincethis preserves the fact that the numerical ordering of nonnegative real numbers corresponds to the lexicographic ordering of their floating-point representations.3 When the exponent is stored in a k bit field, that means that only 2k - 1 values are available for use as exponents, since one must be reserved to represent 0.
Note that the × in a floating-point number is part of the notation, and different from a floating-point multiply operation. The meaning of the × symbol should be clear from the context. For example, the expression (2.5 × 10-3) × (4.0 × 102) involves only a single floating-point multiplication.
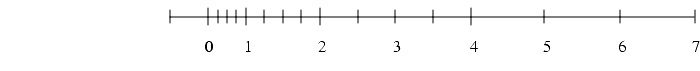
FIGURE D-1 Normalized numbers when
 = 2, p = 3, emin = -1, emax = 2
= 2, p = 3, emin = -1, emax = 2Relative Error and Ulps
Since rounding error is inherent in floating-point computation, it is important to have a way to measure this error. Consider the floating-point format with  = 10 and p = 3, which will be used throughout this section. If the result of a floating-point computation is 3.12 × 10-2, and the answer when computed to infinite precision is .0314, it is clear that this is in error by 2 units in the last place. Similarly, if the real number .0314159 is represented as 3.14 × 10-2, then it is in error by .159 units in the last place. In general, if the floating-point number d.d...d×
= 10 and p = 3, which will be used throughout this section. If the result of a floating-point computation is 3.12 × 10-2, and the answer when computed to infinite precision is .0314, it is clear that this is in error by 2 units in the last place. Similarly, if the real number .0314159 is represented as 3.14 × 10-2, then it is in error by .159 units in the last place. In general, if the floating-point number d.d...d× e is used to represent z, then it is in error by
e is used to represent z, then it is in error by  d.d...d - (z/
d.d...d - (z/ e)
e)
 p-1 units in the last place.4,5 The term ulps will be used as shorthand for "units in the last place." If the result of a calculation is the floating-point number nearest to the correct result, it still might be in error by as much as .5 ulp. Another way to measure the difference between a floating-point number and the real number it is approximating is relative error, which is simply the difference between the two numbers divided by the real number. For example the relative error committed when approximating 3.14159 by 3.14 × 100 is .00159/3.14159
p-1 units in the last place.4,5 The term ulps will be used as shorthand for "units in the last place." If the result of a calculation is the floating-point number nearest to the correct result, it still might be in error by as much as .5 ulp. Another way to measure the difference between a floating-point number and the real number it is approximating is relative error, which is simply the difference between the two numbers divided by the real number. For example the relative error committed when approximating 3.14159 by 3.14 × 100 is .00159/3.14159  .0005.
.0005.
To compute the relative error that corresponds to .5 ulp, observe that when a real number is approximated by the closest possible floating-point numberd.dd...dd × e,the error can be as large as 0.00...00
e,the error can be as large as 0.00...00 ' ×
' ×  e, where
e, where  ' is the digit
' is the digit  /2, there are p units in the significand of the floating-point number, and punits of 0 in the significand of the error. This error is ((
/2, there are p units in the significand of the floating-point number, and punits of 0 in the significand of the error. This error is (( /2)
/2) -p) ×
-p) × e. Since numbers of the form d.dd...dd×
e. Since numbers of the form d.dd...dd× e all have the same absolute error, but have values that range between
e all have the same absolute error, but have values that range between  e and
e and  ×
× e, the relative error ranges between ((
e, the relative error ranges between (( /2)
/2) -p) ×
-p) ×  e/
e/ e and ((
e and (( /2)
/2) -p) ×
-p) ×  e/
e/ e+1. That is,
e+1. That is,
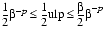
In particular, the relative error corresponding to .5 ulp can vary by a factor of  . This factor is called the wobble. Setting
. This factor is called the wobble. Setting  = (
= ( /2)
/2) -p to the largest of the bounds in (2) above, we can say that when a real number is rounded to the closest floating-point number, the relative error is always bounded by e, which is referred to as machine epsilon.
-p to the largest of the bounds in (2) above, we can say that when a real number is rounded to the closest floating-point number, the relative error is always bounded by e, which is referred to as machine epsilon.
In the example above, the relative error was .00159/3.14159 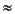 .0005. In order to avoid such small numbers, the relative error is normally written as a factor times
.0005. In order to avoid such small numbers, the relative error is normally written as a factor times  , which in this case is
, which in this case is  = (
= ( /2)
/2) -p = 5(10)-3 = .005. Thus the relative error would be expressed as (.00159/3.14159)/.005)
-p = 5(10)-3 = .005. Thus the relative error would be expressed as (.00159/3.14159)/.005) 
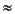 0.1
0.1 .
.
To illustrate the difference between ulps and relative error, consider the real number x = 12.35. It is approximated by  = 1.24 × 101. The error is 0.5 ulps, the relative error is 0.8
= 1.24 × 101. The error is 0.5 ulps, the relative error is 0.8 . Next consider the computation 8
. Next consider the computation 8 . The exact value is 8x = 98.8, while the computed value is 8
. The exact value is 8x = 98.8, while the computed value is 8 = 9.92 × 101. The error is now 4.0 ulps, but the relative error is still 0.8
= 9.92 × 101. The error is now 4.0 ulps, but the relative error is still 0.8 . The error measured in ulps is 8 times larger, even though the relative error is the same. In general, when the base is
. The error measured in ulps is 8 times larger, even though the relative error is the same. In general, when the base is  , a fixed relative error expressed in ulps can wobble by a factor of up to
, a fixed relative error expressed in ulps can wobble by a factor of up to  . And conversely, as equation (2) above shows, a fixed error of .5 ulps results in a relative error that can wobble by
. And conversely, as equation (2) above shows, a fixed error of .5 ulps results in a relative error that can wobble by  .
.
The most natural way to measure rounding error is in ulps. For example rounding to the nearest floating-point number corresponds to an error of less than or equal to .5 ulp. However, when analyzing the rounding error caused by various formulas, relative error is a better measure. A good illustration of this is the analysis in the section Theorem 9. Since  can overestimate the effect of rounding to the nearest floating-point number by the wobble factor of
can overestimate the effect of rounding to the nearest floating-point number by the wobble factor of  , error estimates of formulas will be tighter on machines with a small
, error estimates of formulas will be tighter on machines with a small  .
.
When only the order of magnitude of rounding error is of interest, ulps and  may be used interchangeably, since they differ by at most a factor of
may be used interchangeably, since they differ by at most a factor of  . For example, when a floating-point number is in error by n ulps, that means that the number of contaminated digits is log
. For example, when a floating-point number is in error by n ulps, that means that the number of contaminated digits is log n. If the relative error in a computation is n
n. If the relative error in a computation is n , then
, then
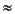 log
log n.
n.Guard Digits
One method of computing the difference between two floating-point numbers is to compute the difference exactly and then round it to the nearest floating-point number. This is very expensive if the operands differ greatly in size. Assuming p = 3, 2.15 × 1012 - 1.25 × 10-5 would be calculated as
- x = 2.15 × 1012
y = .0000000000000000125 × 1012
x - y = 2.1499999999999999875 × 1012
which rounds to 2.15 × 1012. Rather than using all these digits, floating-point hardware normally operates on a fixed number of digits. Suppose that the number of digits kept is p, and that when the smaller operand is shifted right, digits are simply discarded (as opposed to rounding). Then 2.15 × 1012 - 1.25 × 10-5 becomes
- x = 2.15 × 1012
y = 0.00 × 1012
x - y = 2.15 × 1012
The answer is exactly the same as if the difference had been computed exactly and then rounded. Take another example: 10.1 - 9.93. This becomes
- x = 1.01 × 101
y = 0.99 × 101
x - y = .02 × 101
The correct answer is .17, so the computed difference is off by 30 ulps and is wrong in every digit! How bad can the error be?
Theorem 1
- Using a floating-point format with parameters
 andp, and computing differences using pdigits, the relative error of the result can be as large as
andp, and computing differences using pdigits, the relative error of the result can be as large as - 1.
- 1.
Proof
- A relative error of
 - 1 in the expression x - y occurs when x = 1.00...0 and y = .
- 1 in the expression x - y occurs when x = 1.00...0 and y = .
 ...
... , where
, where  =
=  - 1. Here y has p digits (all equal to
- 1. Here y has p digits (all equal to  ). The exact difference is x - y =
). The exact difference is x - y =  -p. However, when computing the answer using only p digits, the rightmost digit of y gets shifted off, and so the computed difference is
-p. However, when computing the answer using only p digits, the rightmost digit of y gets shifted off, and so the computed difference is  -p+1. Thus the error is
-p+1. Thus the error is  -p -
-p -  -p+1 =
-p+1 =  -p (
-p ( - 1), and the relative error is
- 1), and the relative error is  -p(
-p( - 1)/
- 1)/ -p =
-p =  - 1. z
- 1. z
When  =2, the relative error can be as large as the result, and when
=2, the relative error can be as large as the result, and when  =10, it can be 9 times larger. Or to put it another way, when
=10, it can be 9 times larger. Or to put it another way, when  =2, equation (3) shows that the number of contaminated digits is log2(1/
=2, equation (3) shows that the number of contaminated digits is log2(1/ ) = log2(2p) = p. That is, all of the p digits in the result are wrong! Suppose that one extra digit is added to guard against this situation (a guard digit). That is, the smaller number is truncated to p + 1 digits, and then the result of the subtraction is rounded to p digits. With a guard digit, the previous example becomes
) = log2(2p) = p. That is, all of the p digits in the result are wrong! Suppose that one extra digit is added to guard against this situation (a guard digit). That is, the smaller number is truncated to p + 1 digits, and then the result of the subtraction is rounded to p digits. With a guard digit, the previous example becomes
- x = 1.010 × 101
y = 0.993 × 101
x - y = .017 × 101
and the answer is exact. With a single guard digit, the relative error of the result may be greater than  , as in 110 - 8.59.
, as in 110 - 8.59.
- x = 1.10 × 102
y = .085 × 102
x - y = 1.015 × 102
This rounds to 102, compared with the correct answer of 101.41, for a relative error of .006, which is greater than  = .005. In general, the relative error of the result can be only slightly larger than
= .005. In general, the relative error of the result can be only slightly larger than  . More precisely,
. More precisely,
Theorem 2
- If x and y are floating-point numbers in a format with parameters
 and p, and if subtraction is done with p + 1 digits (i.e. one guard digit), then the relative rounding error in the result is less than 2
and p, and if subtraction is done with p + 1 digits (i.e. one guard digit), then the relative rounding error in the result is less than 2 .
.
This theorem will be proven in Rounding Error. Addition is included in the above theorem since x and y can be positive or negative.
Cancellation
The last section can be summarized by saying that without a guard digit, the relative error committed when subtracting two nearby quantities can be very large. In other words, the evaluation of any expression containing a subtraction (or an addition of quantities with opposite signs) could result in a relative error so large that all the digits are meaningless (Theorem 1). When subtracting nearby quantities, the most significant digits in the operands match and cancel each other. There are two kinds of cancellation: catastrophic and benign.
Catastrophic cancellation occurs when the operands are subject to rounding errors. For example in the quadratic formula, the expression b2 - 4ac occurs. The quantities b2 and 4ac are subject to rounding errors since they are the results of floating-point multiplications. Suppose that they are rounded to the nearest floating-point number, and so are accurate to within .5 ulp. When they are subtracted, cancellation can cause many of the accurate digits to disappear, leaving behind mainly digits contaminated by rounding error. Hence the difference might have an error of many ulps. For example, consider b = 3.34, a = 1.22, and c = 2.28. The exact value of b2 - 4ac is .0292. But b2 rounds to 11.2 and 4ac rounds to 11.1, hence the final answer is .1 which is an error by 70 ulps, even though 11.2 - 11.1 is exactly equal to .16. The subtraction did not introduce any error, but rather exposed the error introduced in the earlier multiplications.
Benign cancellation occurs when subtracting exactly known quantities. If x and y have no rounding error, then by Theorem 2 if the subtraction is done with a guard digit, the difference x-y has a very small relative error (less than 2 ).
).
A formula that exhibits catastrophic cancellation can sometimes be rearranged to eliminate the problem. Again consider the quadratic formula
(4)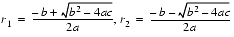
When 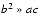 , then
, then 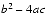 does not involve a cancellation and
does not involve a cancellation and
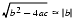 .
. But the other addition (subtraction) in one of the formulas will have a catastrophic cancellation. To avoid this, multiply the numerator and denominator of r1 by
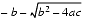
(and similarly for r2) to obtain
(5)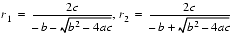
If  and
and 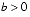 , then computing r1 using formula (4) will involve a cancellation. Therefore, use formula (5) for computing r1 and (4) for r2. On the other hand, if b < 0, use (4) for computing r1 and (5) for r2.
, then computing r1 using formula (4) will involve a cancellation. Therefore, use formula (5) for computing r1 and (4) for r2. On the other hand, if b < 0, use (4) for computing r1 and (5) for r2.
The expression x2 - y2 is another formula that exhibits catastrophic cancellation. It is more accurate to evaluate it as (x - y)(x + y).7 Unlike the quadratic formula, this improved form still has a subtraction, but it is a benign cancellation of quantities without rounding error, not a catastrophic one. By Theorem 2, the relative error in x - y is at most 2 . The same is true of x + y. Multiplying two quantities with a small relative error results in a product with a small relative error (see the section Rounding Error).
. The same is true of x + y. Multiplying two quantities with a small relative error results in a product with a small relative error (see the section Rounding Error).
In order to avoid confusion between exact and computed values, the following notation is used. Whereas x - y denotes the exact difference of x and y, x y denotes the computed difference (i.e., with rounding error). Similarly
y denotes the computed difference (i.e., with rounding error). Similarly 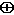 ,
,  , and
, and 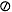 denote computed addition, multiplication, and division, respectively. All caps indicate the computed value of a function, as in or . Lowercase functions and traditional mathematical notation denote their exact values as in ln(x) and
denote computed addition, multiplication, and division, respectively. All caps indicate the computed value of a function, as in or . Lowercase functions and traditional mathematical notation denote their exact values as in ln(x) and 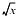 .
.
Although (x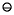 y)
y)  (x
(x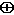 y) is an excellent approximation to x2 - y2, the floating-point numbers x and y might themselves be approximations to some true quantities
y) is an excellent approximation to x2 - y2, the floating-point numbers x and y might themselves be approximations to some true quantities  and
and 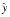 . For example,
. For example, 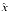 and
and 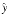 might be exactly known decimal numbers that cannot be expressed exactly in binary. In this case, even though x
might be exactly known decimal numbers that cannot be expressed exactly in binary. In this case, even though x 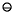 y is a good approximation to x - y, it can have a huge relative error compared to the true expression
y is a good approximation to x - y, it can have a huge relative error compared to the true expression 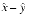 , and so the advantage of (x + y)(x - y) over x2 - y2 is not as dramatic. Since computing (x + y)(x - y) is about the same amount of work as computing x2 - y2, it is clearly the preferred form in this case. In general, however, replacing a catastrophic cancellation by a benign one is not worthwhile if the expense is large, because the input is often (but not always) an approximation. But eliminating a cancellation entirely (as in the quadratic formula) is worthwhile even if the data are not exact. Throughout this paper, it will be assumed that the floating-point inputs to an algorithm are exact and that the results are computed as accurately as possible.
, and so the advantage of (x + y)(x - y) over x2 - y2 is not as dramatic. Since computing (x + y)(x - y) is about the same amount of work as computing x2 - y2, it is clearly the preferred form in this case. In general, however, replacing a catastrophic cancellation by a benign one is not worthwhile if the expense is large, because the input is often (but not always) an approximation. But eliminating a cancellation entirely (as in the quadratic formula) is worthwhile even if the data are not exact. Throughout this paper, it will be assumed that the floating-point inputs to an algorithm are exact and that the results are computed as accurately as possible.
The expression x2 - y2 is more accurate when rewritten as (x - y)(x + y) because a catastrophic cancellation is replaced with a benign one. We next present more interesting examples of formulas exhibiting catastrophic cancellation that can be rewritten to exhibit only benign cancellation.
The area of a triangle can be expressed directly in terms of the lengths of its sides a, b, and c as
(6)
(Suppose the triangle is very flat; that is, a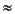 b + c. Then s
b + c. Then s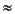 a, and the term (s - a) in formula (6) subtracts two nearby numbers, one of which may have rounding error. For example, if a = 9.0, b = c = 4.53, the correct value of s is 9.03 and A is 2.342.... Even though the computed value of s (9.05) is in error by only 2 ulps, the computed value of A is 3.04, an error of 70 ulps.
a, and the term (s - a) in formula (6) subtracts two nearby numbers, one of which may have rounding error. For example, if a = 9.0, b = c = 4.53, the correct value of s is 9.03 and A is 2.342.... Even though the computed value of s (9.05) is in error by only 2 ulps, the computed value of A is 3.04, an error of 70 ulps.
There is a way to rewrite formula (6) so that it will return accurate results even for flat triangles [Kahan 1986]. It is
(7)
If a, b, and c do not satisfy a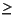 b
b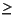 c, rename them before applying (7). It is straightforward to check that the right-hand sides of (6) and (7) are algebraically identical. Using the values of a, b, and c above gives a computed area of 2.35, which is 1 ulp in error and much more accurate than the first formula.
c, rename them before applying (7). It is straightforward to check that the right-hand sides of (6) and (7) are algebraically identical. Using the values of a, b, and c above gives a computed area of 2.35, which is 1 ulp in error and much more accurate than the first formula.
Although formula (7) is much more accurate than (6) for this example, it would be nice to know how well (7) performs in general.
Theorem 3
- The rounding error incurred when using (7) to compute the area of a triangle is at most 11
 , provided that subtraction is performed with a guard digit, e
, provided that subtraction is performed with a guard digit, e 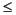 .005, and that square roots are computed to within 1/2 ulp.
.005, and that square roots are computed to within 1/2 ulp.
The condition that e < .005 is met in virtually every actual floating-point system. For example when  = 2, p
= 2, p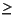 8 ensures that e < .005, and when
8 ensures that e < .005, and when  = 10, p
= 10, p 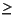 3 is enough.
3 is enough.
In statements like Theorem 3 that discuss the relative error of an expression, it is understood that the expression is computed using floating-point arithmetic. In particular, the relative error is actually of the expression
(8) ((a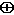 (b
(b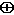 c))
c))  (c
(c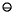 (a
(a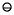 b))
b))  (c
(c 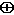 (a
(a 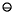 b))
b))  (a
(a 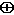 (b
(b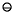 c)))
c)))  4
4Because of the cumbersome nature of (8), in the statement of theorems we will usually say the computed value of E rather than writing out E with circle notation.
Error bounds are usually too pessimistic. In the numerical example given above, the computed value of (7) is 2.35, compared with a true value of 2.34216 for a relative error of 0.7 , which is much less than 11
, which is much less than 11 . The main reason for computing error bounds is not to get precise bounds but rather to verify that the formula does not contain numerical problems.
. The main reason for computing error bounds is not to get precise bounds but rather to verify that the formula does not contain numerical problems.
A final example of an expression that can be rewritten to use benign cancellation is (1 + x)n, where 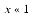 . This expression arises in financial calculations. Consider depositing $100 every day into a bank account that earns an annual interest rate of 6%, compounded daily. If n = 365 and i = .06, the amount of money accumulated at the end of one year is
. This expression arises in financial calculations. Consider depositing $100 every day into a bank account that earns an annual interest rate of 6%, compounded daily. If n = 365 and i = .06, the amount of money accumulated at the end of one year is
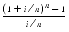
dollars. If this is computed using  = 2 and p = 24, the result is $37615.45 compared to the exact answer of $37614.05, a discrepancy of $1.40. The reason for the problem is easy to see. The expression 1 + i/n involves adding 1 to .0001643836, so the low order bits of i/n are lost. This rounding error is amplified when 1 + i/n is raised to the nth power.
= 2 and p = 24, the result is $37615.45 compared to the exact answer of $37614.05, a discrepancy of $1.40. The reason for the problem is easy to see. The expression 1 + i/n involves adding 1 to .0001643836, so the low order bits of i/n are lost. This rounding error is amplified when 1 + i/n is raised to the nth power.
The troublesome expression (1 + i/n)n can be rewritten as enln(1 + i/n), where now the problem is to compute ln(1 + x) for small x. One approach is to use the approximation ln(1 + x) 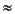 x, in which case the payment becomes $37617.26, which is off by $3.21 and even less accurate than the obvious formula. But there is a way to compute ln(1 + x) very accurately, as Theorem 4 shows [Hewlett-Packard 1982]. This formula yields $37614.07, accurate to within two cents!
x, in which case the payment becomes $37617.26, which is off by $3.21 and even less accurate than the obvious formula. But there is a way to compute ln(1 + x) very accurately, as Theorem 4 shows [Hewlett-Packard 1982]. This formula yields $37614.07, accurate to within two cents!
Theorem 4 assumes that approximates ln(x) to within 1/2 ulp. The problem it solves is that when x is small, (1 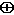 x) is not close to ln(1 + x) because 1
x) is not close to ln(1 + x) because 1 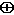 x has lost the information in the low order bits of x. That is, the computed value of ln(1 + x) is not close to its actual value when
x has lost the information in the low order bits of x. That is, the computed value of ln(1 + x) is not close to its actual value when 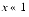 .
.
Theorem 4
- If ln(1 + x) is computed using the formula

- the relative error is at most 5
 when 0
when 0 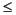 x < 3/4, provided subtraction is performed with a guard digit, e < 0.1, and ln is computed to within 1/2 ulp.
x < 3/4, provided subtraction is performed with a guard digit, e < 0.1, and ln is computed to within 1/2 ulp.
This formula will work for any value of x but is only interesting for 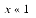 , which is where catastrophic cancellation occurs in the naive formula ln(1 + x). Although the formula may seem mysterious, there is a simple explanation for why it works. Write ln(1 + x) as
, which is where catastrophic cancellation occurs in the naive formula ln(1 + x). Although the formula may seem mysterious, there is a simple explanation for why it works. Write ln(1 + x) as
 .
. The left hand factor can be computed exactly, but the right hand factor µ(x) = ln(1 + x)/x will suffer a large rounding error when adding 1 to x. However, µ is almost constant, since ln(1 + x) 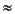 x. So changing x slightly will not introduce much error. In other words, if
x. So changing x slightly will not introduce much error. In other words, if  , computing
, computing  will be a good approximation to xµ(x) = ln(1 + x). Is there a value for
will be a good approximation to xµ(x) = ln(1 + x). Is there a value for 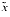 for which
for which  and
and 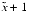 can be computed accurately? There is; namely
can be computed accurately? There is; namely 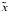 = (1
= (1 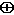 x)
x) 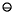 1, because then 1 +
1, because then 1 +  is exactly equal to 1
is exactly equal to 1 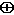 x.
x.
The results of this section can be summarized by saying that a guard digit guarantees accuracy when nearby precisely known quantities are subtracted (benign cancellation). Sometimes a formula that gives inaccurate results can be rewritten to have much higher numerical accuracy by using benign cancellation; however, the procedure only works if subtraction is performed using a guard digit. The price of a guard digit is not high, because it merely requires making the adder one bit wider. For a 54 bit double precision adder, the additional cost is less than 2%. For this price, you gain the ability to run many algorithms such as formula (6) for computing the area of a triangle and the expression ln(1 + x). Although most modern computers have a guard digit, there are a few (such as Cray systems) that do not.
Exactly Rounded Operations
When floating-point operations are done with a guard digit, they are not as accurate as if they were computed exactly then rounded to the nearest floating-point number. Operations performed in this manner will be called exactly rounded.8 The example immediately preceding Theorem 2 shows that a single guard digit will not always give exactly rounded results. The previous section gave several examples of algorithms that require a guard digit in order to work properly. This section gives examples of algorithms that require exact rounding.
So far, the definition of rounding has not been given. Rounding is straightforward, with the exception of how to round halfway cases; for example, should 12.5 round to 12 or 13? One school of thought divides the 10 digits in half, letting {0, 1, 2, 3, 4} round down, and {5, 6, 7, 8, 9} round up; thus 12.5 would round to 13. This is how rounding works on Digital Equipment Corporation's VAX computers. Another school of thought says that since numbers ending in 5 are halfway between two possible roundings, they should round down half the time and round up the other half. One way of obtaining this 50% behavior to require that the rounded result have its least significant digit be even. Thus 12.5 rounds to 12 rather than 13 because 2 is even. Which of these methods is best, round up or round to even? Reiser and Knuth [1975] offer the following reason for preferring round to even.
Theorem 5
- Let x and y be floating-point numbers, and define x0 = x, x1 = (x0
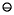 y)
y) 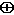 y, ..., xn = (xn-1
y, ..., xn = (xn-1  y)
y) 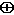 y. If
y. If 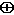 and
and 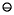 are exactly rounded using round to even, then either xn = x for all n or xn = x1 for all n
are exactly rounded using round to even, then either xn = x for all n or xn = x1 for all n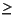 1. z
1. z
To clarify this result, consider  = 10, p = 3 and let x = 1.00, y = -.555. When rounding up, the sequence becomes
= 10, p = 3 and let x = 1.00, y = -.555. When rounding up, the sequence becomes
 y = 1.56, x1 = 1.56
y = 1.56, x1 = 1.56  .555 = 1.01, x1
.555 = 1.01, x1 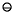 y = 1.01
y = 1.01 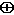 .555 = 1.57,
.555 = 1.57,and each successive value of xn increases by .01, until xn = 9.45 (n  845)9. Under round to even, xn is always 1.00. This example suggests that when using the round up rule, computations can gradually drift upward, whereas when using round to even the theorem says this cannot happen. Throughout the rest of this paper, round to even will be used.
845)9. Under round to even, xn is always 1.00. This example suggests that when using the round up rule, computations can gradually drift upward, whereas when using round to even the theorem says this cannot happen. Throughout the rest of this paper, round to even will be used.
One application of exact rounding occurs in multiple precision arithmetic. There are two basic approaches to higher precision. One approach represents floating-point numbers using a very large significand, which is stored in an array of words, and codes the routines for manipulating these numbers in assembly language. The second approach represents higher precision floating-point numbers as an array of ordinary floating-point numbers, where adding the elements of the array in infinite precision recovers the high precision floating-point number. It is this second approach that will be discussed here. The advantage of using an array of floating-point numbers is that it can be coded portably in a high level language, but it requires exactly rounded arithmetic.
The key to multiplication in this system is representing a product xy as a sum, where each summand has the same precision as x and y. This can be done by splitting x and y. Writing x = xh + xl and y = yh + yl, the exact product is
xy = xh yh + xhyl + xlyh + xlyl.If x and y have p bit significands, the summands will also have p bit significands provided that xl, xh, yh, yl can be represented using [p/2] bits. When p is even, it is easy to find a splitting. The number x0.x1...xp - 1 can be written as the sum of x0.x1 ... xp/2 - 1 and 0.0 ... 0xp/2...xp - 1. When p is odd, this simple splitting method will not work. An extra bit can, however, be gained by using negative numbers. For example, if  = 2, p = 5, and x = .10111, x can be split as xh = .11 and xl = -.00001. There is more than one way to split a number. A splitting method that is easy to compute is due to Dekker [1971], but it requires more than a single guard digit.
= 2, p = 5, and x = .10111, x can be split as xh = .11 and xl = -.00001. There is more than one way to split a number. A splitting method that is easy to compute is due to Dekker [1971], but it requires more than a single guard digit.
Theorem 6
- Let p be the floating-point precision, with the restriction that p is even when
 > 2, and assume that floating-point operations are exactly rounded. Then if k = [p/2] is half the precision (rounded up) and m =
> 2, and assume that floating-point operations are exactly rounded. Then if k = [p/2] is half the precision (rounded up) and m =  k + 1, x can be split as x = xh + xl, where
k + 1, x can be split as x = xh + xl, where
 x)
x)  (m
(m  x
x  x), xl = x
x), xl = x  xh,
xh, and each xi is representable using [p/2] bits of precision.
To see how this theorem works in an example, let  = 10, p = 4, b = 3.476, a = 3.463, and c = 3.479. Then b2 - ac rounded to the nearest floating-point number is .03480, while b
= 10, p = 4, b = 3.476, a = 3.463, and c = 3.479. Then b2 - ac rounded to the nearest floating-point number is .03480, while b b = 12.08, a
b = 12.08, a c = 12.05, and so the computed value of b2 - ac is .03. This is an error of 480 ulps. Using Theorem 6 to write b = 3.5 - .024, a = 3.5 - .037, and c = 3.5 - .021, b2 becomes 3.52 - 2 × 3.5 × .024 + .0242. Each summand is exact, so b2 = 12.25 - .168 + .000576, where the sum is left unevaluated at this point. Similarly, ac = 3.52 - (3.5 × .037 + 3.5 × .021) + .037 × .021 = 12.25 - .2030 +.000777. Finally, subtracting these two series term by term gives an estimate for b2 - ac of 0
c = 12.05, and so the computed value of b2 - ac is .03. This is an error of 480 ulps. Using Theorem 6 to write b = 3.5 - .024, a = 3.5 - .037, and c = 3.5 - .021, b2 becomes 3.52 - 2 × 3.5 × .024 + .0242. Each summand is exact, so b2 = 12.25 - .168 + .000576, where the sum is left unevaluated at this point. Similarly, ac = 3.52 - (3.5 × .037 + 3.5 × .021) + .037 × .021 = 12.25 - .2030 +.000777. Finally, subtracting these two series term by term gives an estimate for b2 - ac of 0 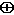 .0350
.0350 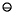 .000201 = .03480, which is identical to the exactly rounded result. To show that Theorem 6 really requires exact rounding, consider p = 3,
.000201 = .03480, which is identical to the exactly rounded result. To show that Theorem 6 really requires exact rounding, consider p = 3,  = 2, and x = 7. Then m = 5, mx = 35, and m
= 2, and x = 7. Then m = 5, mx = 35, and m  x = 32. If subtraction is performed with a single guard digit, then (m
x = 32. If subtraction is performed with a single guard digit, then (m  x)
x) 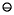 x = 28. Therefore, xh = 4 and xl = 3, hence xl is not representable with [p/2] = 1 bit.
x = 28. Therefore, xh = 4 and xl = 3, hence xl is not representable with [p/2] = 1 bit.
As a final example of exact rounding, consider dividing m by 10. The result is a floating-point number that will in general not be equal to m/10. When  = 2, multiplying m/10 by 10 will restore m, provided exact rounding is being used. Actually, a more general fact (due to Kahan) is true. The proof is ingenious, but readers not interested in such details can skip ahead to section The IEEE Standard.
= 2, multiplying m/10 by 10 will restore m, provided exact rounding is being used. Actually, a more general fact (due to Kahan) is true. The proof is ingenious, but readers not interested in such details can skip ahead to section The IEEE Standard.
Theorem 7
- When
 = 2, if m and n are integers with |m| < 2p - 1 and n has the special form n = 2i + 2j, then (m
= 2, if m and n are integers with |m| < 2p - 1 and n has the special form n = 2i + 2j, then (m  n)
n)  n = m, provided floating-point operations are exactly rounded.
n = m, provided floating-point operations are exactly rounded.
Proof
- Scaling by a power of two is harmless, since it changes only the exponent, not the significand. If q = m/n, then scale n so that 2p - 1
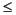 n < 2p and scale m so that 1/2 < q < 1. Thus, 2p - 2 < m < 2p. Since m has p significant bits, it has at most one bit to the right of the binary point. Changing the sign of m is harmless, so assume that q > 0.
n < 2p and scale m so that 1/2 < q < 1. Thus, 2p - 2 < m < 2p. Since m has p significant bits, it has at most one bit to the right of the binary point. Changing the sign of m is harmless, so assume that q > 0. - If
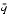 = m
= m 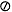 n, to prove the theorem requires showing that
n, to prove the theorem requires showing that
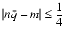
- That is because m has at most 1 bit right of the binary point, so n
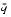 will round to m. To deal with the halfway case when |n
will round to m. To deal with the halfway case when |n - m| = 1/4, note that since the initial unscaled m had |m| < 2p - 1, its low-order bit was 0, so the low-order bit of the scaled m is also 0. Thus, halfway cases will round to m.
- m| = 1/4, note that since the initial unscaled m had |m| < 2p - 1, its low-order bit was 0, so the low-order bit of the scaled m is also 0. Thus, halfway cases will round to m. - Suppose that q = .q1q2..., and let
 = .q1q2...qp1. To estimate |n
= .q1q2...qp1. To estimate |n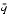 - m|, first compute
- m|, first compute
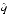 - q| = |N/2p + 1 - m/n|,
- q| = |N/2p + 1 - m/n|, - where N is an odd integer. Since n = 2i + 2j and 2p - 1
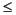 n < 2p, it must be that n = 2p - 1 + 2k for some k
n < 2p, it must be that n = 2p - 1 + 2k for some k 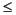 p - 2, and thus
p - 2, and thus
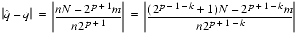 .
.- The numerator is an integer, and since N is odd, it is in fact an odd integer. Thus,
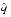 - q|
- q|  1/(n2p + 1 - k).
1/(n2p + 1 - k). - Assume q <
 (the case q >
(the case q >  is similar).10 Then n
is similar).10 Then n < m, and
< m, and
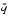 |= m-n
|= m-n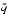 = n(q-
= n(q-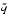 ) = n(q-(
) = n(q-(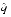 -2-p-1))
-2-p-1))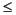

=(2p-1+2k)2-p-1-2-p-1+k =
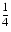
- This establishes (9) and proves the theorem.11z
The theorem holds true for any base  , as long as 2i + 2j is replaced by
, as long as 2i + 2j is replaced by  i +
i +  j. As
j. As  gets larger, however, denominators of the form
gets larger, however, denominators of the form  i +
i +  j are farther and farther apart.
j are farther and farther apart.
We are now in a position to answer the question, Does it matter if the basic arithmetic operations introduce a little more rounding error than necessary? The answer is that it does matter, because accurate basic operations enable us to prove that formulas are "correct" in the sense they have a small relative error. The section Cancellation discussed several algorithms that require guard digits to produce correct results in this sense. If the input to those formulas are numbers representing imprecise measurements, however, the bounds of Theorems 3 and 4 become less interesting. The reason is that the benign cancellation x - y can become catastrophic if x and y are only approximations to some measured quantity. But accurate operations are useful even in the face of inexact data, because they enable us to establish exact relationships like those discussed in Theorems 6 and 7. These are useful even if every floating-point variable is only an approximation to some actual value.
The IEEE Standard
There are two different IEEE standards for floating-point computation. IEEE 754 is a binary standard that requires  = 2, p = 24 for single precision and p = 53 for double precision [IEEE 1987]. It also specifies the precise layout of bits in a single and double precision. IEEE 854 allows either
= 2, p = 24 for single precision and p = 53 for double precision [IEEE 1987]. It also specifies the precise layout of bits in a single and double precision. IEEE 854 allows either  = 2 or
= 2 or  = 10 and unlike 754, does not specify how floating-point numbers are encoded into bits [Cody et al. 1984]. It does not require a particular value for p, but instead it specifies constraints on the allowable values of p for single and double precision. The term IEEE Standard will be used when discussing properties common to both standards.
= 10 and unlike 754, does not specify how floating-point numbers are encoded into bits [Cody et al. 1984]. It does not require a particular value for p, but instead it specifies constraints on the allowable values of p for single and double precision. The term IEEE Standard will be used when discussing properties common to both standards.
This section provides a tour of the IEEE standard. Each subsection discusses one aspect of the standard and why it was included. It is not the purpose of this paper to argue that the IEEE standard is the best possible floating-point standard but rather to accept the standard as given and provide an introduction to its use. For full details consult the standards themselves [IEEE 1987; Cody et al. 1984].
Formats and Operations
Base
It is clear why IEEE 854 allows  = 10. Base ten is how humans exchange and think about numbers. Using
= 10. Base ten is how humans exchange and think about numbers. Using  = 10 is especially appropriate for calculators, where the result of each operation is displayed by the calculator in decimal.
= 10 is especially appropriate for calculators, where the result of each operation is displayed by the calculator in decimal.
There are several reasons why IEEE 854 requires that if the base is not 10, it must be 2. The section Relative Error and Ulps mentioned one reason: the results of error analyses are much tighter when  is 2 because a rounding error of .5 ulp wobbles by a factor of
is 2 because a rounding error of .5 ulp wobbles by a factor of  when computed as a relative error, and error analyses are almost always simpler when based on relative error. A related reason has to do with the effective precision for large bases. Consider
when computed as a relative error, and error analyses are almost always simpler when based on relative error. A related reason has to do with the effective precision for large bases. Consider  = 16, p = 1 compared to
= 16, p = 1 compared to  = 2, p = 4. Both systems have 4 bits of significand. Consider the computation of 15/8. When
= 2, p = 4. Both systems have 4 bits of significand. Consider the computation of 15/8. When  = 2, 15 is represented as 1.111 × 23, and 15/8 as 1.111 × 20. So 15/8 is exact. However, when
= 2, 15 is represented as 1.111 × 23, and 15/8 as 1.111 × 20. So 15/8 is exact. However, when  = 16, 15 is represented as F× 160, where F is the hexadecimal digit for 15. But 15/8 is represented as 1 × 160, which has only one bit correct. In general, base 16 can lose up to 3 bits, so that a precision of p hexadecimal digits can have an effective precision as low as 4p - 3 rather than 4p binary bits. Since large values of
= 16, 15 is represented as F× 160, where F is the hexadecimal digit for 15. But 15/8 is represented as 1 × 160, which has only one bit correct. In general, base 16 can lose up to 3 bits, so that a precision of p hexadecimal digits can have an effective precision as low as 4p - 3 rather than 4p binary bits. Since large values of  have these problems, why did IBM choose
have these problems, why did IBM choose  = 16 for its system/370? Only IBM knows for sure, but there are two possible reasons. The first is increased exponent range. Single precision on the system/370 has
= 16 for its system/370? Only IBM knows for sure, but there are two possible reasons. The first is increased exponent range. Single precision on the system/370 has  = 16, p = 6. Hence the significand requires 24 bits. Since this must fit into 32 bits, this leaves 7 bits for the exponent and one for the sign bit. Thus the magnitude of representable numbers ranges from about
= 16, p = 6. Hence the significand requires 24 bits. Since this must fit into 32 bits, this leaves 7 bits for the exponent and one for the sign bit. Thus the magnitude of representable numbers ranges from about  to about
to about 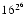 =
= 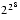 . To get a similar exponent range when
. To get a similar exponent range when  = 2 would require 9 bits of exponent, leaving only 22 bits for the significand. However, it was just pointed out that when
= 2 would require 9 bits of exponent, leaving only 22 bits for the significand. However, it was just pointed out that when  = 16, the effective precision can be as low as 4p - 3 = 21 bits. Even worse, when
= 16, the effective precision can be as low as 4p - 3 = 21 bits. Even worse, when  = 2 it is possible to gain an extra bit of precision (as explained later in this section), so the
= 2 it is possible to gain an extra bit of precision (as explained later in this section), so the  = 2 machine has 23 bits of precision to compare with a range of 21 - 24 bits for the
= 2 machine has 23 bits of precision to compare with a range of 21 - 24 bits for the  = 16 machine.
= 16 machine.
Another possible explanation for choosing  = 16 has to do with shifting. When adding two floating-point numbers, if their exponents are different, one of the significands will have to be shifted to make the radix points line up, slowing down the operation. In the
= 16 has to do with shifting. When adding two floating-point numbers, if their exponents are different, one of the significands will have to be shifted to make the radix points line up, slowing down the operation. In the  = 16, p = 1 system, all the numbers between 1 and 15 have the same exponent, and so no shifting is required when adding any of the (
= 16, p = 1 system, all the numbers between 1 and 15 have the same exponent, and so no shifting is required when adding any of the ( ) = 105 possible pairs of distinct numbers from this set. However, in the
) = 105 possible pairs of distinct numbers from this set. However, in the  = 2, p = 4 system, these numbers have exponents ranging from 0 to 3, and shifting is required for 70 of the 105 pairs.
= 2, p = 4 system, these numbers have exponents ranging from 0 to 3, and shifting is required for 70 of the 105 pairs.
In most modern hardware, the performance gained by avoiding a shift for a subset of operands is negligible, and so the small wobble of  = 2 makes it the preferable base. Another advantage of using
= 2 makes it the preferable base. Another advantage of using  = 2 is that there is a way to gain an extra bit of significance.12 Since floating-point numbers are always normalized, the most significant bit of the significand is always 1, and there is no reason to waste a bit of storage representing it. Formats that use this trick are said to have a hidden bit. It was already pointed out in Floating-point Formats that this requires a special convention for 0. The method given there was that an exponent of emin - 1 and a significand of all zeros represents not
= 2 is that there is a way to gain an extra bit of significance.12 Since floating-point numbers are always normalized, the most significant bit of the significand is always 1, and there is no reason to waste a bit of storage representing it. Formats that use this trick are said to have a hidden bit. It was already pointed out in Floating-point Formats that this requires a special convention for 0. The method given there was that an exponent of emin - 1 and a significand of all zeros represents not  , but rather 0.
, but rather 0.
What’s New in the Actual Windows Guard v1.5 serial key or number?
Screen Shot
System Requirements for Actual Windows Guard v1.5 serial key or number
- First, download the Actual Windows Guard v1.5 serial key or number
-
You can download its setup from given links:


